We have created many Truchet style patterns over the past couple of years and just when we think we may have exhausted this method for building patterns we find another way to extend and complicate!

Every previous Truchet pattern we have made has been a tiling of regular polygons where every side of every polygon has the same number of connection points and has connected the same colour at each point. In this way any tile can be rotated and placed next to any other tile with the sides matching up. A quick glance at our work shows that we have made 11 previous works which have included this type of Truchet pattern. We were feeling like we had maybe exhausted it...

We thought about possible variations and decided to try a simple square tile but with a different number of connection points on each side. Having a choice of 1, 2, 3 or 4 points on each side meant 70 possibilities after eliminating rotations. That was a lot of tiles but we just wanted to see what patterns would emerge so we got to work.

To start with we only made 1 version of each tile which meant that we had to make artistic decisions about each design. We chose to do that rather than have the tiles themselves being generated as we felt the end result would be more aesthetically pleasing. So we made 70 tiles. Here are a few of them.

After some experimentation with the tiles we knew that we wanted to colour each enclosed shape randomly. To do this we created a system where each new tile placed would check the colours of the tile above it and to the left of it and use these colours to fill adjacent areas. Areas on the bottom and the right of each new tile would be filled randomly.

We added extension pieces to each side to create a frame.

To determine the placement of tiles we had created arrays randomly filled with the numbers 1, 2, 3 and 4. So in the above example the top horizontal joins are 4, 1, 1, 3 and the first line of vertical joins are 4, 2, 4, 1, 1.

We experimented with different ways of restricting these numbers to create different effects.

Here are some examples with resricted tile choices.

We also played with other ways of restricting the tile choices to create patterns which would contain some repetition, rotation or reflection without becoming uniform.

We called this feature, 'Demi Random'.

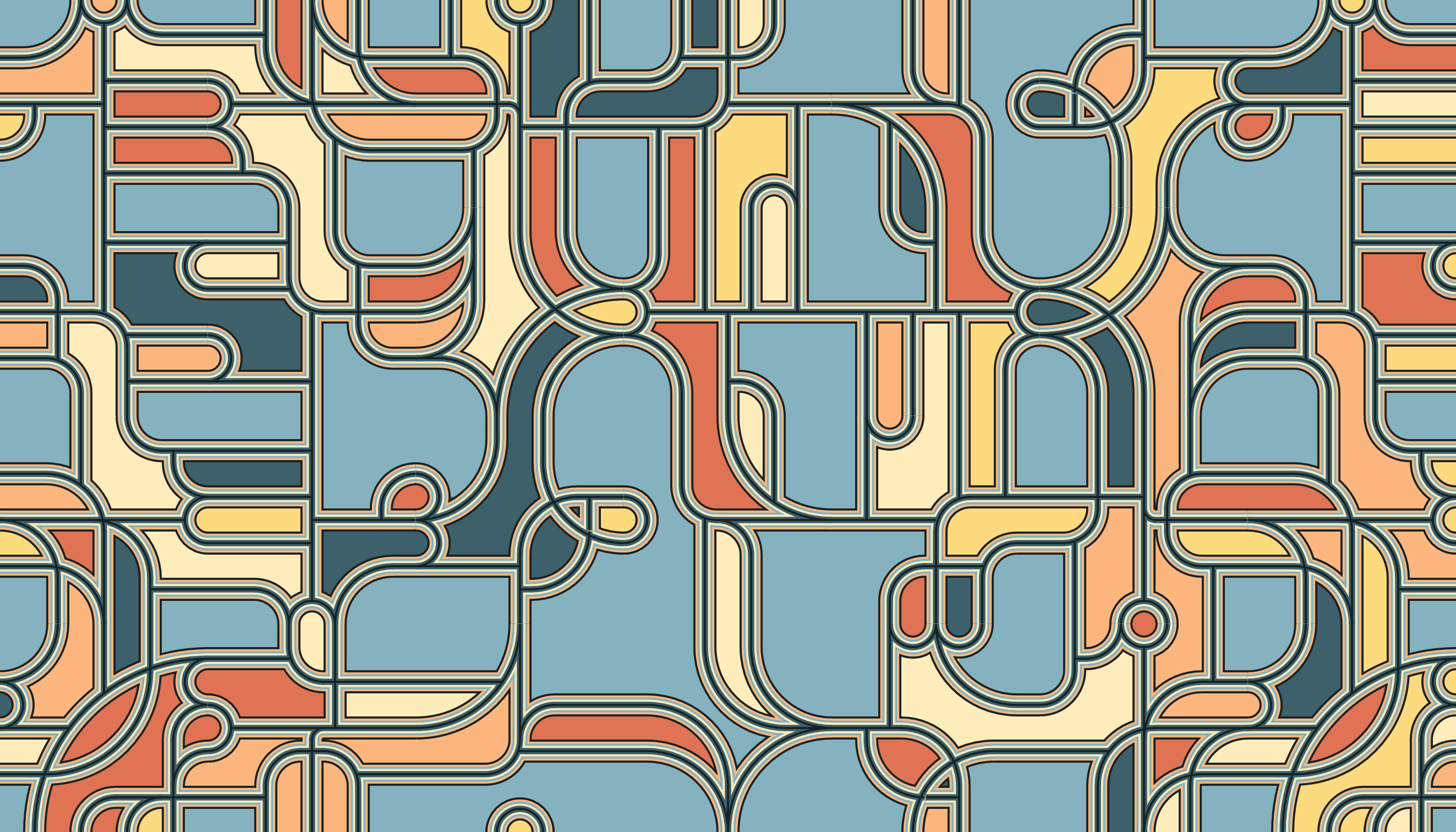
Some outputs of the final piece.